Apéndice C — Conjunto de Datos

El objetivo de este apéndice es listar los conjuntos de datos utilizados en el curso.

Paquetes usados

from sklearn.datasets import load_breast_cancer,\
                             load_diabetes,\
                             load_digits, load_iris,\
                             load_wine
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition
from scipy.stats import multivariate_normal
import umap
from matplotlib import pylab as plt
import matplotlib as mpl
import numpy as np
import pandas as pd
import seaborn as sns

C.1 Problemas Sintéticos

En esta sección se presentan los problemas sintéticos que corresponden aquellos problemas en los que se conocen todos los parámetros y se usan para mostrar algunas características de los algoritmos.

C.2 Mezcla de Clases

p1 = multivariate_normal(mean=[5, 5],
                         cov=[[4, 0], [0, 2]])
X_1 = p1.rvs(size=1000)
p2 = multivariate_normal(mean=[1.5, -1.5],
                         cov=[[2, 1], [1, 3]])
X_2 = p2.rvs(size=1000)
p3 = multivariate_normal(mean=[12.5, -3.5],
                         cov=[[2, 3], [3, 7]])
X_3 = p3.rvs(size=1000)

Figura C.1 muestra estas tres distribuciones.

Código

D = np.concatenate((X_1, X_2, X_3))
clase = [1] * 1000 + [2] * 1000 + [3] * 1000
D = np.concatenate((D, np.atleast_2d(clase).T), axis=1)
df = pd.DataFrame(D, columns=['x', 'y', 'clase'])
_ = sns.relplot(data=df, kind='scatter', x='x',
                palette=PALETTE,
                y='y', hue='clase')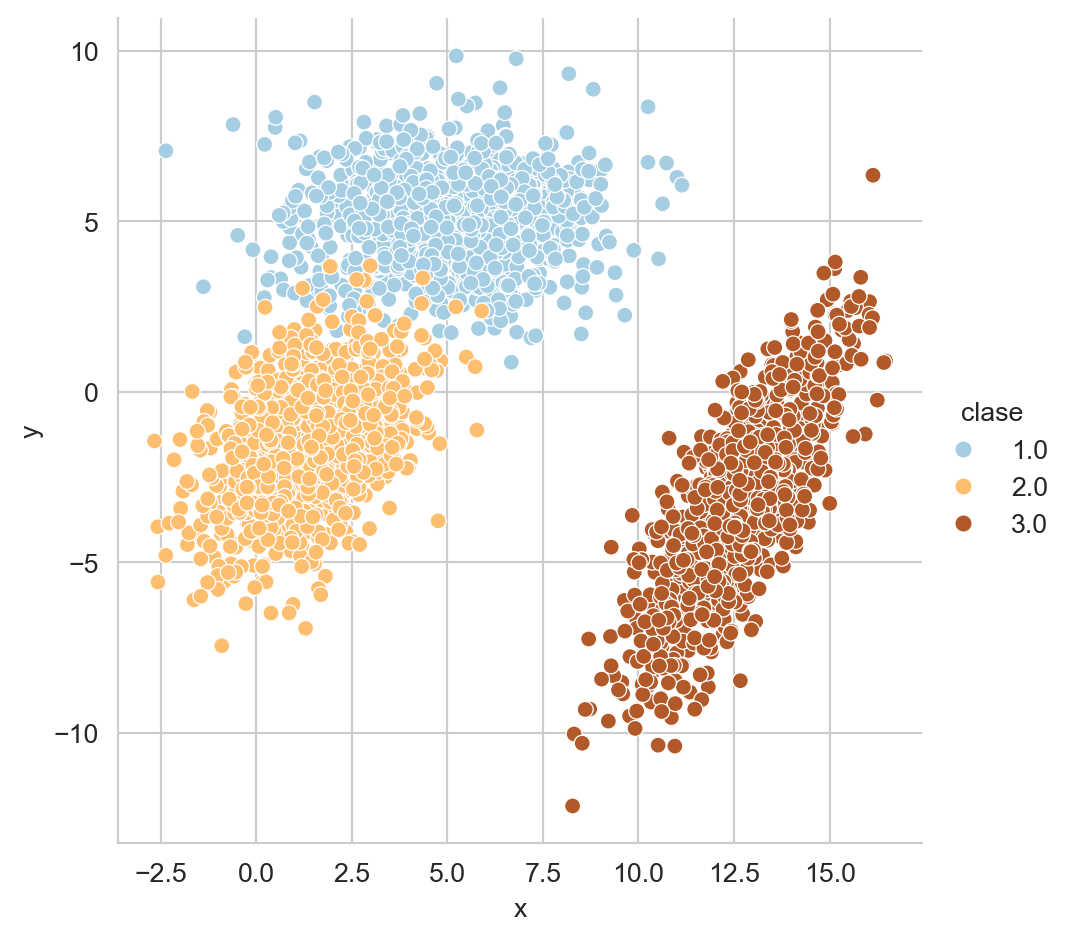

Figura C.1: Muestras de 3 distribuciones gausianas

C.2.1 Clases Separadas

X_1 = multivariate_normal(mean=[5, 5],
                          cov=[[4, 0], [0, 2]]).rvs(1000)
X_2 = multivariate_normal(mean=[-5, -10],
                          cov=[[2, 1], [1, 3]]).rvs(1000)
X_3 = multivariate_normal(mean=[15, -6],
                          cov=[[2, 3], [3, 7]]).rvs(1000)

Este problema se muestra en la Figura C.2.

Código

D = np.concatenate((X_1, X_2, X_3))
clase = [1] * 1000 + [2] * 1000 + [3] * 1000
D = np.concatenate((D, np.atleast_2d(clase).T), axis=1)
df = pd.DataFrame(D, columns=['x', 'y', 'clase'])
_ = sns.relplot(data=df, kind='scatter', x='x',
                palette=PALETTE,
                y='y', hue='clase')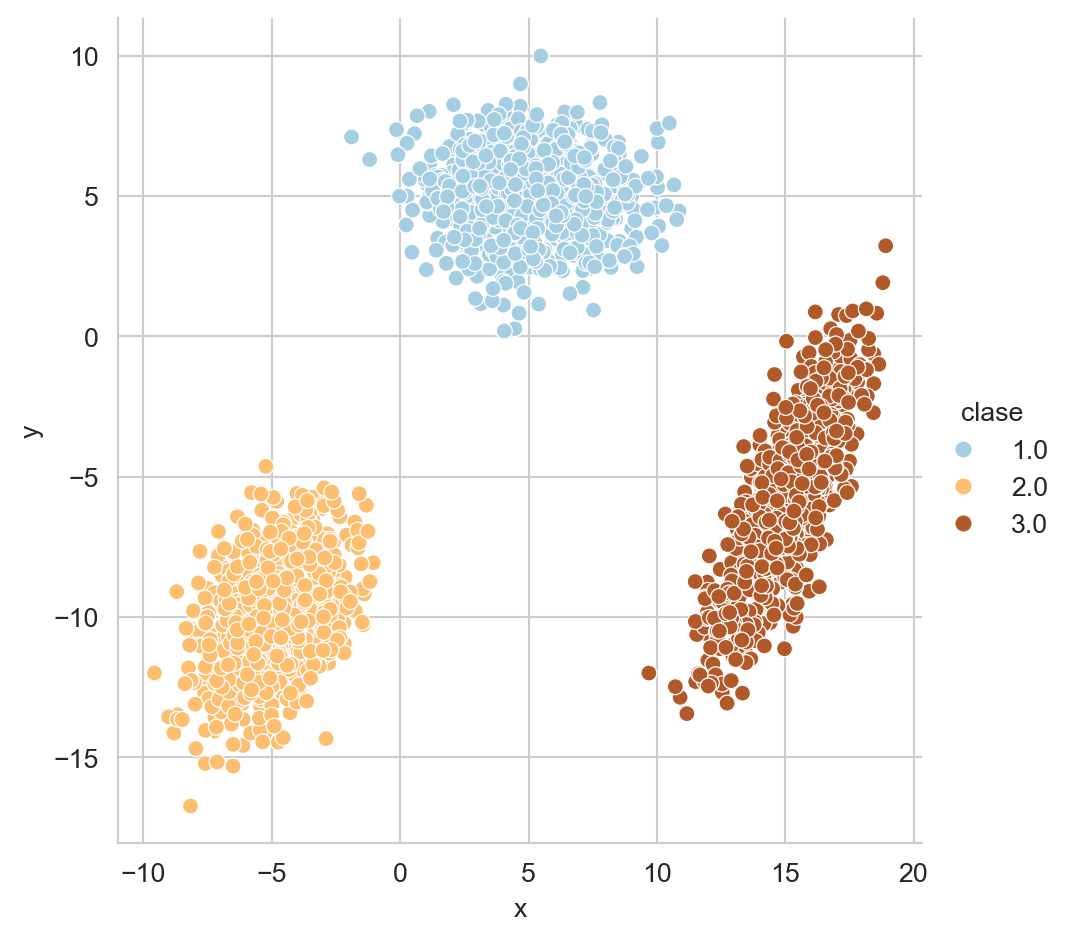

Figura C.2: Muestras de 3 distribuciones gausianas

C.3 Problemas de Clasificación

En esta sección se listan los problemas de clasificación utilizados durante el curso. La Tabla C.1 resume las principales características de los problemas utilizados. Se incluye la entropía como una media que está relacionada al desbalance de clases, la entropía está normalizada para que su rango se encuentre entre \([0, 1].\)

Tabla C.1: Problemas de clasificación

Nombre	Tamaño (\(N\))	Dimensión (\(d\))	Número de clases (\(K\))	Entropía
Breast Cancer	\(569\)	\(30\)	\(2\)	0.95
Iris	\(150\)	\(4\)	\(3\)	1.00
Dígitos	\(1797\)	\(64\)	\(10\)	1.00
Vino	\(178\)	\(13\)	\(3\)	0.99

C.3.1 Breast Cancer Wisconsin

El conjunto de datos de Breast Cancer Wisconsin (ver Street, Wolberg, y Mangasarian (1993)) se obtiene con el siguiente código. La Figura C.3 muestra una proyección utilizando PCA de este conjunto de datos.

D, y = load_breast_cancer(return_X_y=True)

Código

D = StandardScaler().fit_transform(D)
pca = decomposition.PCA(n_components=2).fit(D)
low_dim = pca.transform(D)
# reducer = umap.UMAP(n_neighbors=5)
# low_dim = reducer.fit_transform(D)
df = pd.DataFrame(low_dim, columns=['x', 'y'])
df['Clase'] = y
fig = sns.relplot(df, kind='scatter', 
                  legend='full',  # palette=pal,
                   x='x', y='y', hue='Clase')
fig.tick_params(bottom=False, top=False, 
                left=False, right=False,
                labelbottom=False, labelleft=False)
_ = fig.set(xlabel=None, ylabel=None)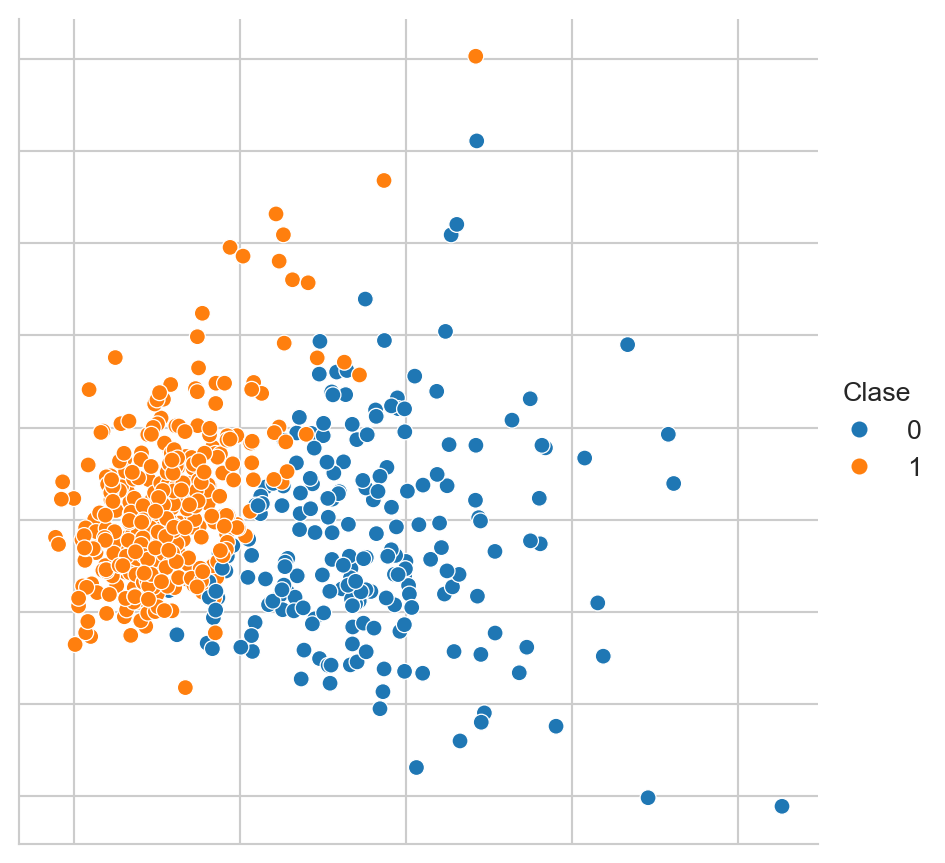

Figura C.3: Proyección mediante PCA del problema de Breast Cancer Wisconsin.

C.3.2 Iris

Un conjunto clásico en problemas de clasificación es el problema del Iris descrito por Fisher (1936); este problema se descarga con la siguiente instrucción. La Figura C.4 muestra una visualización de estos datos mediante PCA.

D, y = load_iris(return_X_y=True)

Código

D = StandardScaler().fit_transform(D)
pca = decomposition.PCA(n_components=2).fit(D)
low_dim = pca.transform(D)
# reducer = umap.UMAP(n_neighbors=5)
# low_dim = reducer.fit_transform(D)
df = pd.DataFrame(low_dim, columns=['x', 'y'])
df['Clase'] = y
fig = sns.relplot(df, kind='scatter', 
                  legend='full', palette=PALETTE,
                   x='x', y='y', hue='Clase')
fig.tick_params(bottom=False, top=False, 
                left=False, right=False,
                labelbottom=False, labelleft=False)
_ = fig.set(xlabel=None, ylabel=None)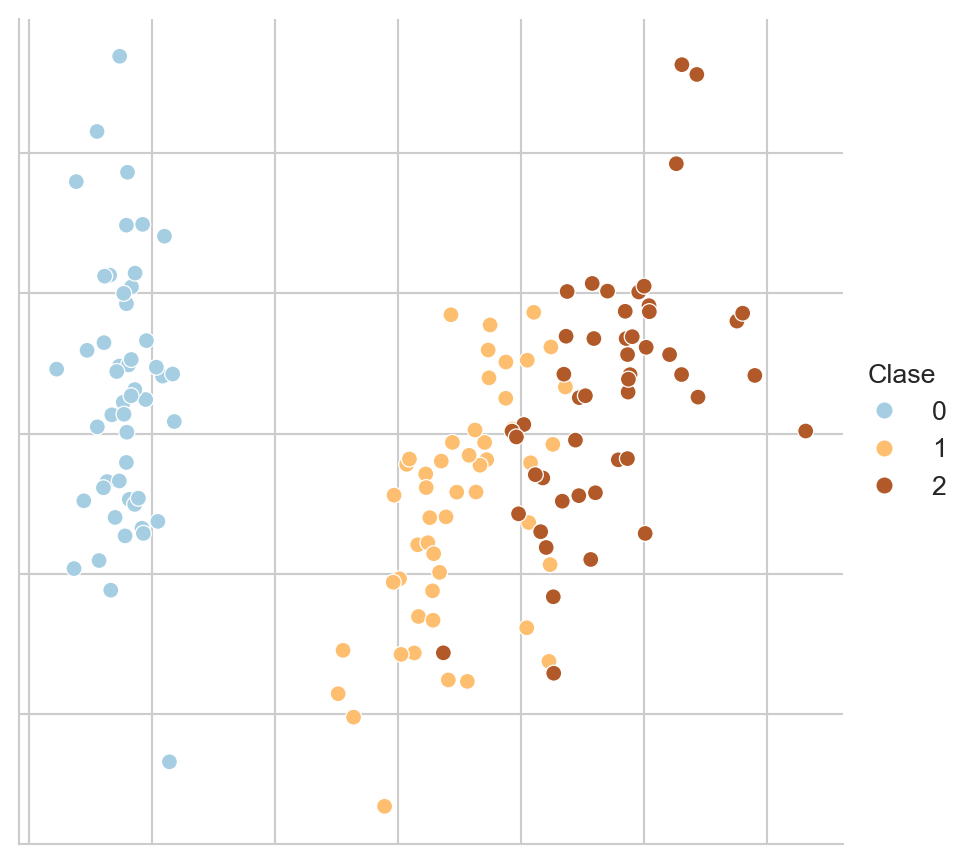

Figura C.4: Proyección mediante PCA del problema del Iris.

C.3.3 Dígitos

El conjunto de Dígitos (ver Xu, Krzyzak, y Suen (1992)) es un conjunto de clasificación donde se trata de identificar el número escrito en una imagen; este conjunto de datos se descarga utilizando la siguiente instrucción. La Figura C.5 muestra una proyección de estos datos utilizando UMAP con ocho vecinos.

D, y = load_digits(return_X_y=True)

Código

pal = mpl.cm.Paired
reducer = umap.UMAP(n_neighbors=8)
D = StandardScaler().fit_transform(D)
low_dim = reducer.fit_transform(D)
df = pd.DataFrame(low_dim, columns=['x', 'y'])
df['Clase'] = y
fig = sns.relplot(df, kind='scatter', 
                  legend='full', palette=PALETTE,
                   x='x', y='y', hue='Clase')
fig.tick_params(bottom=False, top=False, 
                left=False, right=False,
                labelbottom=False, labelleft=False)
_ = fig.set(xlabel=None, ylabel=None)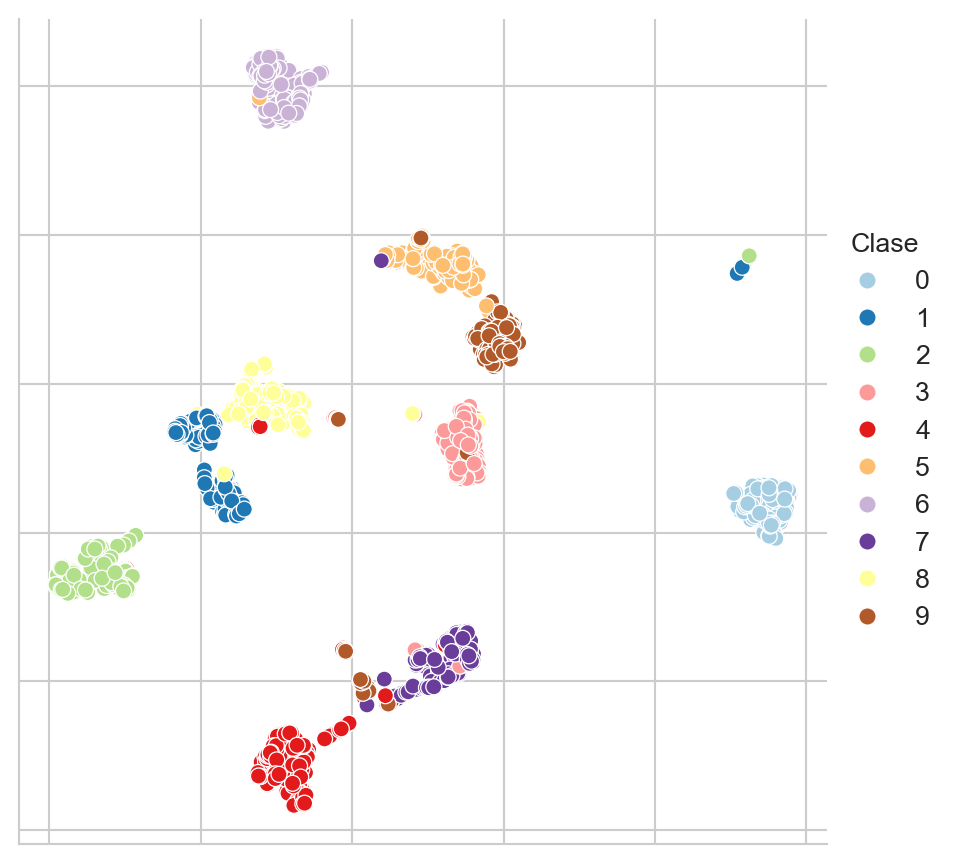

Figura C.5: Proyección mediante UMAP del problema de Dígitos con ocho vecinos.

C.3.4 Vino

El conjunto de Vino se obtiene con la siguiente instrucción. La Figura C.6 muestra una proyección de estos datos utilizando PCA.

D, y = load_wine(return_X_y=True)

Código

pal = mpl.cm.Paired
D = StandardScaler().fit_transform(D)
pca = decomposition.PCA(n_components=2).fit(D)
low_dim = pca.transform(D)
# reducer = umap.UMAP(n_neighbors=5)
# low_dim = reducer.fit_transform(D)
df = pd.DataFrame(low_dim, columns=['x', 'y'])
df['Clase'] = y
fig = sns.relplot(df, kind='scatter', 
                  legend='full', palette=PALETTE,
                   x='x', y='y', hue='Clase')
fig.tick_params(bottom=False, top=False, 
                left=False, right=False,
                labelbottom=False, labelleft=False)
_ = fig.set(xlabel=None, ylabel=None)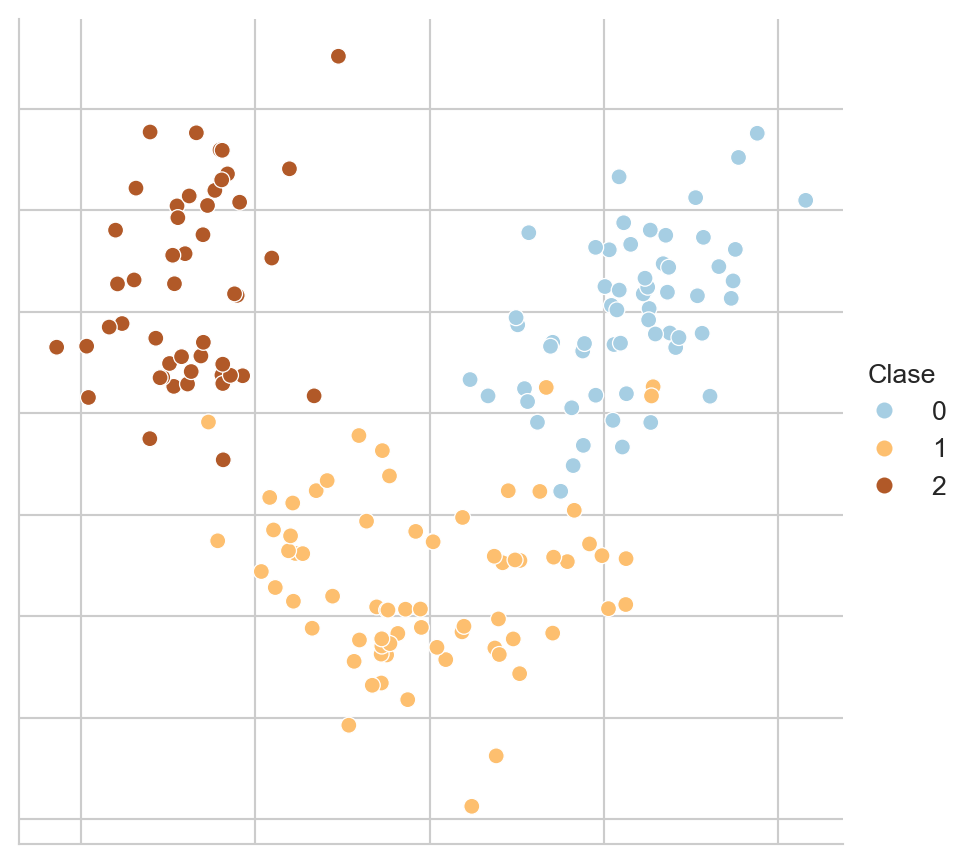

Figura C.6: Proyección mediante PCA del problema del Vino.

C.4 Problemas de Regresión

En esta sección se listan los problemas de regresión utilizados para ejemplificar los algoritmos y su rendimiento.

C.4.1 Problema Sintético

El siguiente ejemplo es un problema de regresión sintético que se forma de la suma de dos funciones trascendentales como se muestra en el siguiente código.

X = np.linspace(-5, 5, 100)
y = np.sin(X) + 0.3 * np.cos(X * 3.)

La Figura C.7 muestra este problema sintético.

Código

df = pd.DataFrame(dict(X=X, y=y))
df.set_index('X', inplace=True)
fig = sns.relplot(df, kind='line')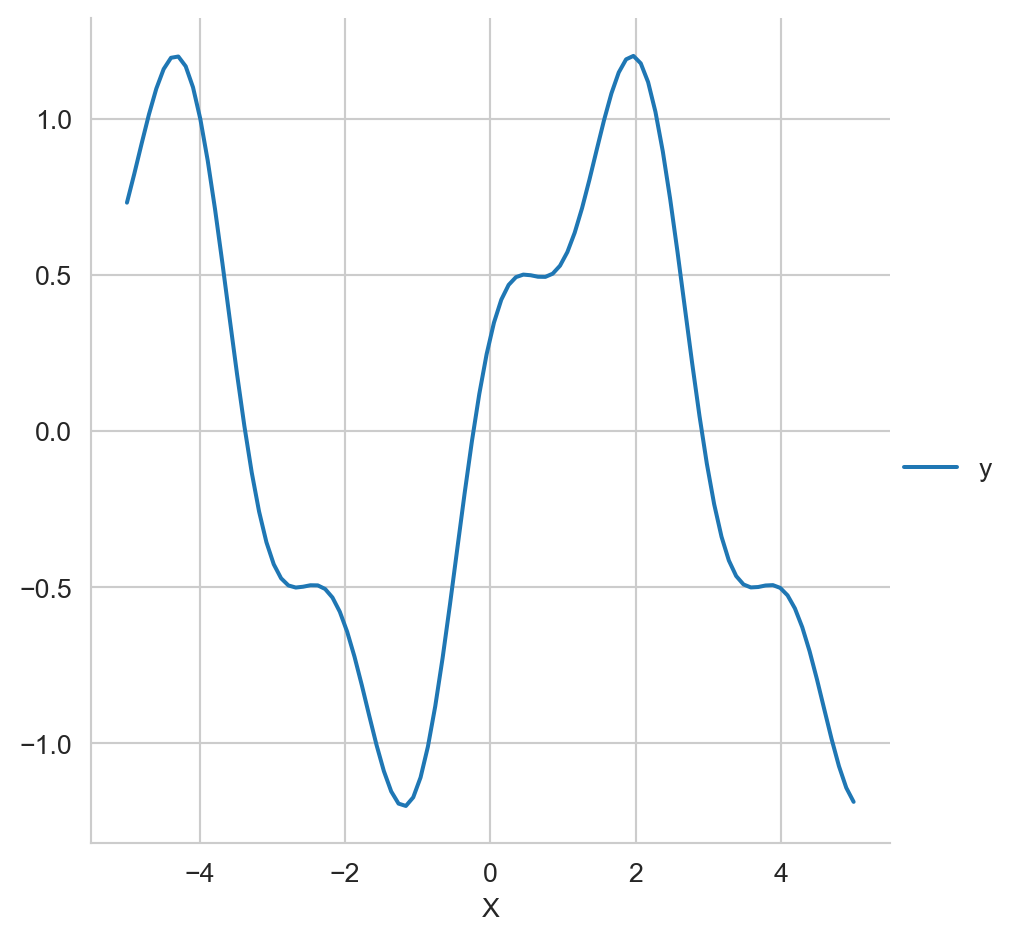

Figura C.7: Problema de Regresión

C.4.2 Diabetes

El conjunto de datos Diabetes es un problema que se puederecuperar usando el siguiente código.

D, y = load_diabetes(return_X_y=True)

Fisher, Ronald Aylmer. 1936. «The use of multiple measurements in taxonomic problems». Annals of Eugenics 7 (2): 179-88. https://doi.org/https://doi.org/10.1111/j.1469-1809.1936.tb02137.x.

Street, William Nick, William H. Wolberg, y Olvi L. Mangasarian. 1993. «Nuclear feature extraction for breast tumor diagnosis». En Electronic imaging. https://api.semanticscholar.org/CorpusID:14922543.

Xu, L., A. Krzyzak, y C. Y. Suen. 1992. «Methods of combining multiple classifiers and their applications to handwriting recognition». IEEE Transactions on Systems, Man, and Cybernetics 22 (3): 418-35. https://doi.org/10.1109/21.155943.